According to Newtonian mechanics, it is not hard to prove the following proposition.
Proposition 1 (The principle of Minimum Potential Energy). For conservative structural systems, of all the kinematically admissible deformations, those corresponding to the equilibrium state extremize (i.e., minimize or maximize) the total potential energy. If the extremum is a minimum, the equilibrium state is stable.
Sometimes it is instructive to solve optimization problems in mathematics by introducing some well-designed physical systems. With the help of the surface tension system, we will prove the following theorem.
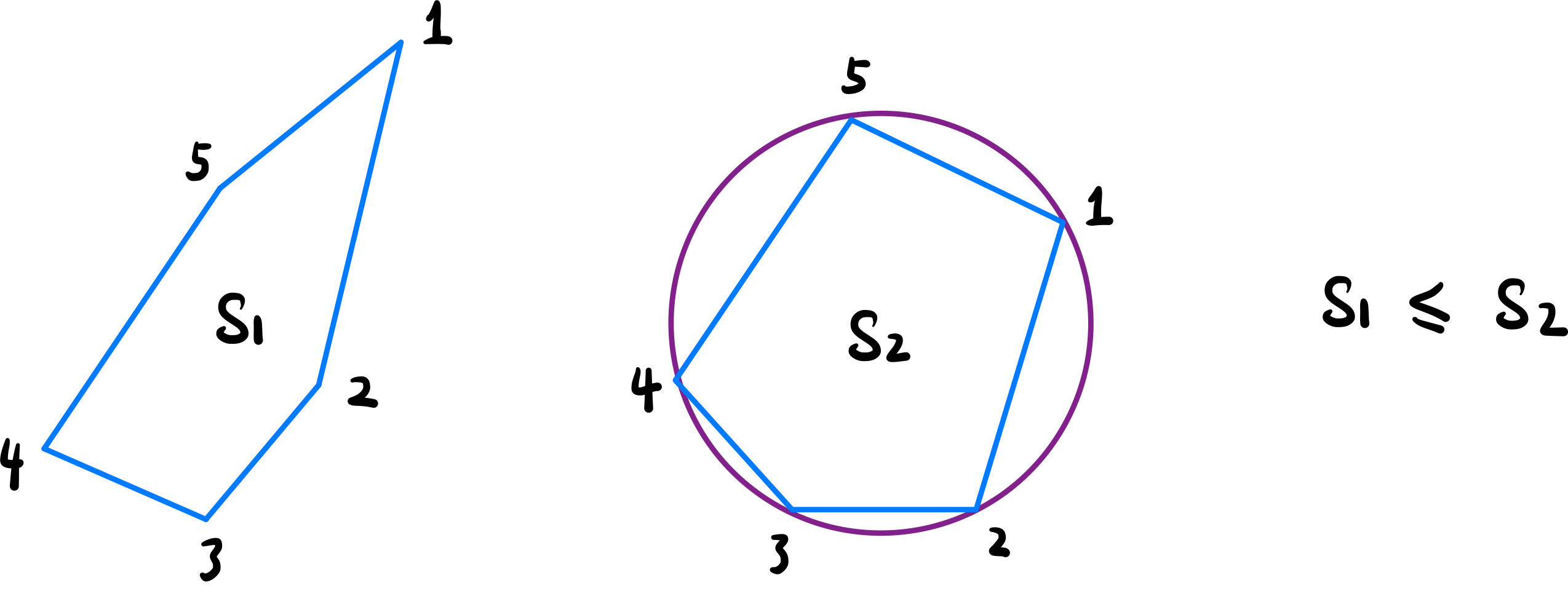
Theorem 1. Among all n-gons with a given side length, the one inscribed in a circle has the largest area.

The physical system we would like to get use of is the surface tension system. Surface tension is the force required to resist to maintain the shape of a soap bubble. The soap bubble always makes its area as small as possible, and surface tension is a manifestation of this tendency.
We will consider the linear surface tension model. As shown in figure 1, for example, suppose there is a rectangular wire with an opening on one side, on which a movable wire of length \ell is installed. A soap bubble is attached between the wires. Suppose there is no friction, then to maintain the size of the soap bubble, a force of magnitude F = \sigma \ell is required whose direction is perpendicular to the wire.
More generally, for soap bubbles of any shape, let d\ell be an infinitesimal line segment of the boundary of the bubble. We will assume that the infinitesimal surface tension on d\ell is \sigma d\ell, and the direction is perpendicular to d\vec{\ell}.
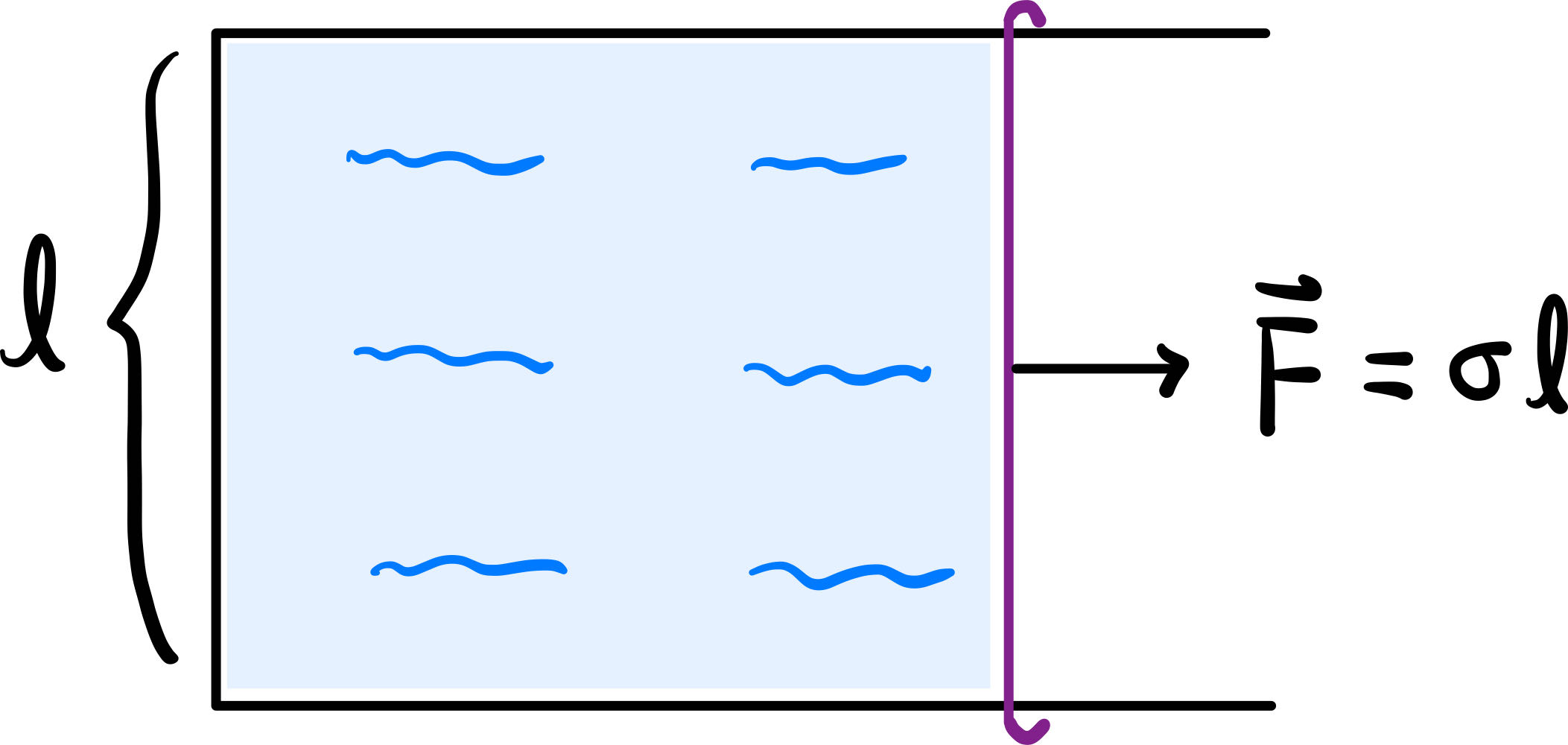
The potential energy of the system shown in figure 1 is clearly E_p = \sigma S, where S is the area of the bubble. This is because, for an infinitesimal movement \Delta x of the purple wire, the work done by surface tension is \Delta W = - \sigma \ell \Delta x = - \sigma \Delta S, so the variation of potential energy is just \Delta E_p = - \Delta W = \sigma \Delta S.
More generally, for a soap bubble of any shape, the potential energy of surface tension is also E_p = \sigma S, with S the area of the bubble. This can be easily seen by analyzing the work done by an infinitesimal segment d\ell of the boundary of the bubble. The only way for d\ell to do some work is to move perpendicular to itself, that is, to increase the area of the surface.
Let us make a wire polygon frame with the given side length. The vertices of the frame are smooth hinges. One can embed the wire into a flat bubble, as shown in figure 2.

Now, the potential energy of this system is from surface tension, that is, E_p = \sigma S, where S is the area of the bubble. By proposition 1, when the system is in equilibrium, the area of the bubble should be minimized, which means the area of the polygon should be maximized.
Let us analyze the constraining forces provided by the hinges when the system is in equilibrium. As shown in figure 3, consider one of the sides, on which the surface tension is \vec{F}_1. Let the constraining forces of the hinges on the two vertices of that side be \vec{f}_1 and \vec{f}_2. It is clear that \vec{f}_1 and \vec{f}_2 must be symmetric about the axis where \vec{F}_1 is located.
Since the hinges are massless, the two constraining forces provided by one hinge acting on two sides must be equal in magnitude and opposite in direction, like \vec{f}_1 and \vec{f}'_1 in figure 3. Thus all the constraining forces have the same magnitude.
Considering the direction of the constraining forces, there are two possibilities as shown in figure 3. The first possibility is that one of \vec{f}_1 and \vec{f}'_1 points inside the polygon, while the second case is that both \vec{f}_1 and \vec{f}'_1 point outside. We claim that only the second case can happen. Without loss of generality, let us assume that \vec{f}_1 is pointing inside the polygon. Then \vec{f}'_1 together with \vec{f}_3 and \vec{F}_2 can not keep the side they act on in balance, where \vec{F}_2 is the surface tension, and \vec{f}_3 is the constraining forces symmetric with \vec{f}'_1 with respect to \vec{F}_2. So only the second possibility is physically correct.

Now, let us take a closer look at the angles between the constraining forces and the sides. As shown in figure 4, when the system is in equilibrium, \theta_1 should satisfy 2f \sin \theta_1 = F_1 = \sigma \ell_1, where f = f_1 = f_2 is the magnitude of the constraining forces, and \ell_1 is the length of the side under consideration.

If we now make perpendiculars to \vec{f}_1 and \vec{f}_2, we will get an isosceles triangle with waist length r. We have r = \frac{\ell_1}{2 \sin \theta_1} = \frac{f}{\sigma}, which is independent of the length of the side. Note that one can do a similar analysis for adjacent sides, and it is not hard to find that the polygon is inscribed in a circle of radius r!

A direct corollary is that for a plane figure with a certain side length, the circle has the largest area. One can just embed a rope into the bubble to show this.
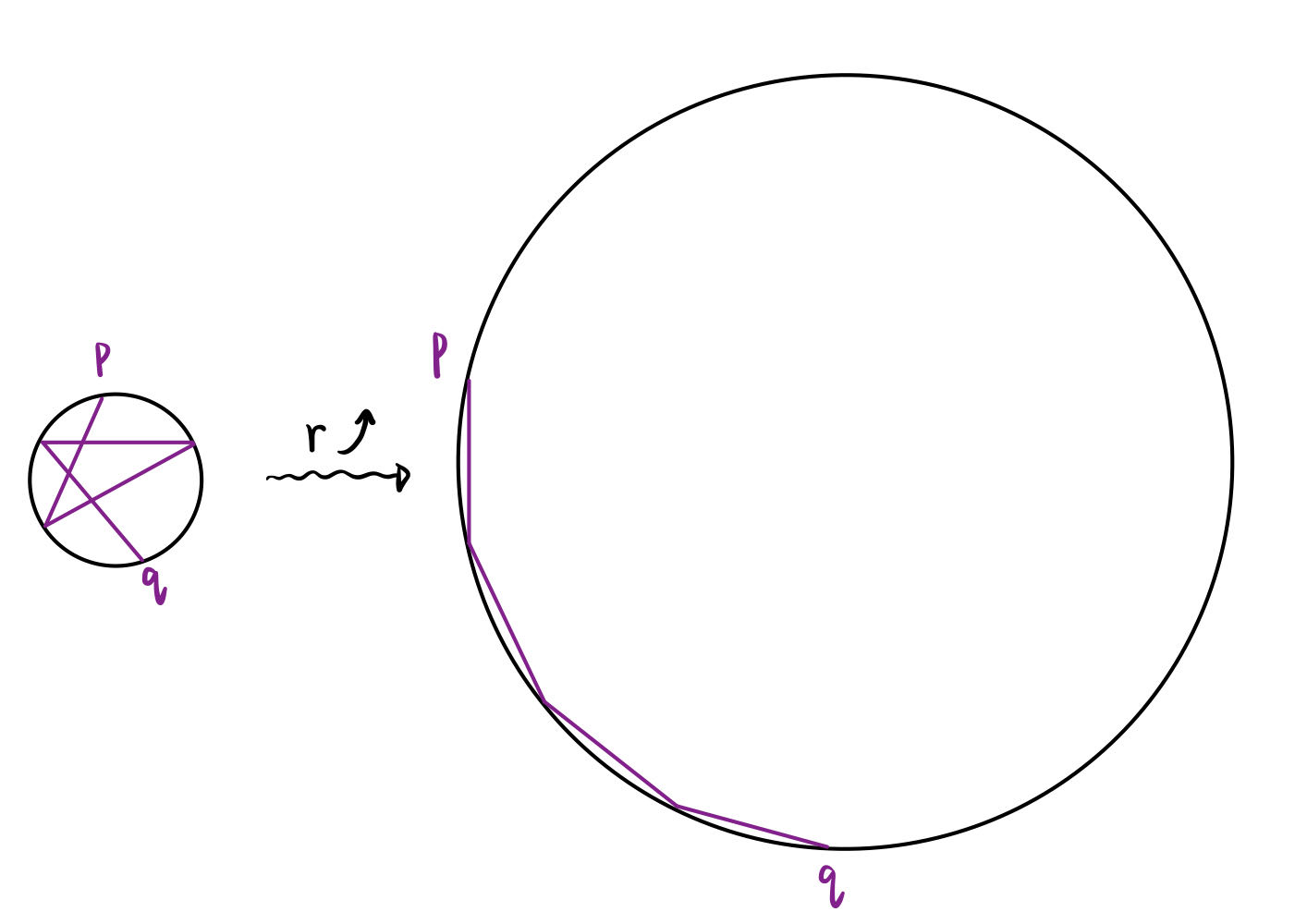
Note that our proof does not manifest that the extremum is a minimum. This can be shown by arguing that the circumcircle exists and is unique. As shown in figure 6, we can open one of the hinges and attach the remaining hinges to a circle of radius r, where 2r is equal to the length of the longest side. If the two endpoints p and q meet, then the circle is the circumcircle. If not, then we can slowly increase r and denote the angle between p and q by \Theta(r). In the beginning, \Theta(r) is greater than 2\pi. When r is too large, as shown in figure 6, \Theta(r) is smaller than 2\pi. It is clear that \Theta(r) is a strictly decreasing continuous function of r. Thus there exists a unique r^* such that \Theta(r^*) = 2\pi, and the radius of the circumcircle is just r^*.
The combination of physics and mathematics is always beautiful!